V_tb

Index:

• Introduction
• Method and code
• Updated plots
• Recommendations
• Publications
• Talks
• Authors

Introduction:

R (= BR(t->Wb)/BR(t->Wq)) and single top cross section provide valuable informations on |V_ti|.
Both CDF and D0 published limits on |V_tb| based on the assumption that σ(s+t observed)=|V_tb|²σ(s+t theory [Standard Model]). This is correct only in the limit |V_tb|>>|V_td|,|V_ts|, i.e. R~1. Current measurements indicate R large, but still with a large error, which still allows some room for d and s quark densities to contribute to the initial state of t-channel single top production, making a bit more complicated the extraction of |V_tb| from single top.
Here we expose our proposal for a model-independent extraction of |V_tb| from the simultaneous combination of R and single top results. This is not to be intended as a real physics result, since we have no access to the Tevatron data and we can use only the published results, which forces us to several rough approximations (detailed in the next section).

Method and code:

Download the macro histos.C
Usage (in ROOT): .L histos.C ; vti()

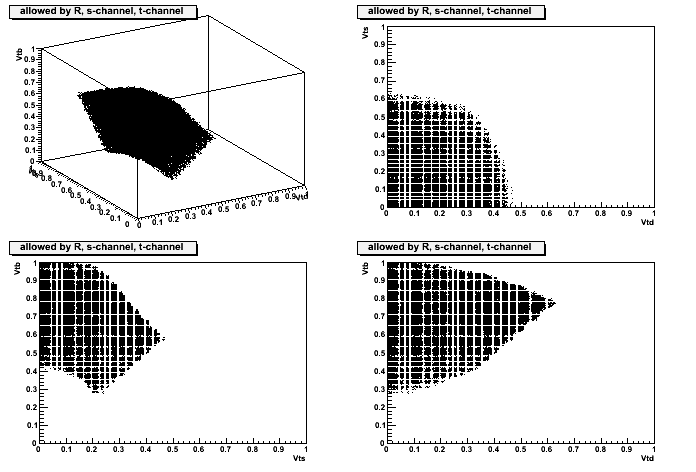
This macro simply plots the regions in {V_td,V_ts,V_tb} allowed by the measurements of R and of s-channel and t-channel (separately) single top cross section.
The formulas used to relate {R,σ(s),σ(t)} with {V_td,V_ts,V_tb} are:

• R = |V_tb|²/(|V_td|²+|V_ts|²+|V_tb|²)
• σ(s) = R*|V_tb|²*σ(s | theory, SM)
• σ(t) = R*{|V_td|²*α_d*σ(t | theory, incoming d) + |V_ts|²*α_s*σ(t | theory, incoming s) + |V_tb|²*α_b*σ(t | theory, SM) + 2*β*(|V_td|²+|V_ts|²)*σ(s | theory, SM)}
• σ(single top) = σ(s)+σ(t)

These formulas take into account the fact that, in case of non-negligible coupling with d or s, an s-channel final state (Wbq or Wqb) resembles a t-channel and will more probably fall in this cathegory than in the proper one.
On the other hand, it will not always be tagged as a t-channel event: the SM assumption is deeply embedded in the Tevatron analyses through the training of the multivariate discriminators (NN, LR, BDT, ...), and for example an s-channel event with t->Wq decay, classified as background by the s-channel search due to the presence of only one b-jet, could be classified as background by the t-channel search as well because the W would be paired to the only b-jet to form a top candidate, while the correct pairing would be with the light jet. Also the angular distribution of the light jet would be "wrong".
This is reflected by the β factor in the third formula, whose value is somewhere between ~1/2 and 1. The macro asks β as input, and the plots in this page use β=1.
Similar remarks lead to the inclusion of the α_x coefficients, since the event kinematics depend on the incoming quark. Nevertheless, this dependence is expected to be quite small. The macro asks the α_x's as input, and the plots in this page use α_x=1 for each x.

The macro simply bins the {V_td,V_ts,V_tb} space and checks for each bin if it is allowed by the experimental constraints given as input. The 95% CL limit for R and the 2σ limits for single top are used (note: 95% CL corresponds to 1.96σ, to be exact).
The trivial constraint |V_td|²+|V_ts|²+|V_tb|² <= 1 is also applied.
It has to be noted that a proper treatment would require taking into account the correlations between R and single top errors. These are certainly large, but unfortunately with no access to data we have no means to estimate them.

In the macro it is possible to choose whether to use the total single top cross section, or the individual s- and t-channel measurements. In principle the latter option is more informative, but in practice the s-/t-channel separation is still too poor to be really helpful. (When more statistics will permit to improve them, it will be mandatory to take into account the anti-correlation between s- and t-channel individual measurements.)

Updated plots:

CDF data (from here)

R > 0.61 @ 95% CL, with 160/pb
σ(single top, s+t) = 2.2+-0.7 pb
σ(s-channel) = 1.6^+0.9_-0.8 pb
σ(t-channel) = 0.8^+0.7_-0.6 pb

These plots assume β=1, and use the total single top cross section (s+t):

Plots with only the R constraint, only the single top (s+t) constraint, only the s-channel constraint, only the t-channel constraint.

D0 data (from here)

R > 0.79 @ 95% CL, with 0.9/fb
σ(single top, s+t) = 4.7+-1.3 pb
σ(s-channel) = 1.0+-0.9 pb
σ(t-channel) = 4.2^+1.8_-1.4 pb

These plots assume β=1, and use the total single top cross section (s+t):

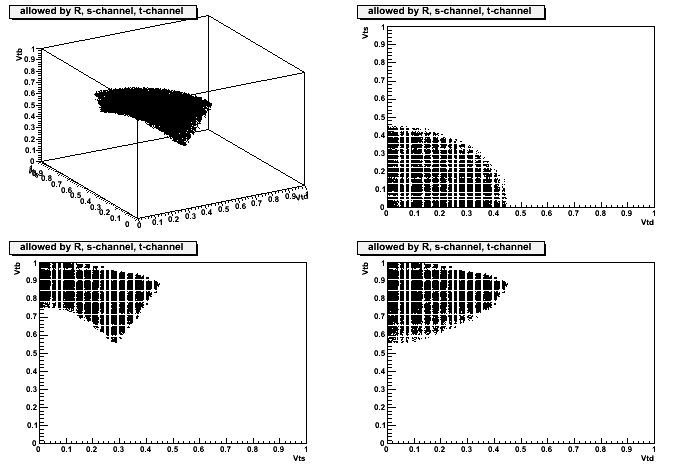
Plots with only the R constraint, only the single top (s+t) constraint, only the s-channel constraint, only the t-channel constraint.

Recommendations:

• Use of MC generators with full CKM dependence; examples are MadGraph (LO+PS), ZTOP (pure NLO) and MC@NLO (NLO+PS). This will permit to extract the α_x and β efficiency factors that we had to guess-stimate here.
• R<1 would have an effect also on ttbar background, not only on signal!
• R and single top measurements are certainly correlated to some extent. This has to be taken into account.

Publications:

• "Is V_tb~1?", hep-ph/0607115, Eur.Phys.J. C 49, 791-801 (2007)
• Updated in "Collider aspects of flavour physics at high Q", arXiv:0801.1800 (Section 2.2)

Talks:

• R.Frederix, 2008/5/20 at TOP2008
• E.Kou, 2006/5/15 at "FLAVOUR IN THE ERA OF THE LHC"