Spin:
σ(A+B -> C+D) = k_CD(2S_C+1)(2S_D+1)P_C²T_if
where k_CD=1/2 if C=D, 1 otherwise; T_if is the square of the spin averaged transition amplitude.
This formula was used to extract the spin of the charged pion, using the reactions π⁺d -> pp and pp -> π⁺d (the spins of proton and deuton were already known).
For the neutral pion, the existence of the decay into 2 photons proves that the spin has to be integer (0 or 1) since the photon spin is 1.
But 1 is forbidden for the pion, for the following reason:
in the pion rest frame, the 2 photons are back-to-back; let's take their common direction as quantization axis; along this axis, their spins can combine only to give 0 or 2.
Anyway, it's observed that positive, negative and neutral pions are produced in equal number, so the spin quantum number has to be the same for all three.

Parity of the charged pion:
The parity of a 2-particle state is (-1)^L times P(1) times P(2).
Method: Negative pions are stopped in a deuterium target. They form a pionic atom and quickly reach the S-state, where the overlap of their wave-function with the nucleus is maximal. At that point the reaction π^-d -> nn.
Initial state: The deuteron has S=1. The pion has S=0 (see above). The pion/deuteron S-state has L=0. As a consequence, J=1 (and, being conserved, J=1 also for the final state).
Deuteron has P=+1: in fact, P(p)*P(n)=+1, but deuteron has spin 1 and so, considering the orbital motion of the proton and neutron, L+S=1 and (-1)^L+S+1=+1.
Since (-1)^L=+1 (S-state) and P(d)=+1, the parity of the pion is the same of the final state.
Final state: it has to be antisymmetric for exchange of the two neutrons, since they are identical fermions. But the isospin wavefunction is symmetric.
The spin can be S=0 (antisymmetric combination, since the neutron spins are antiparallel) or S=1 (symmetric, spins are parallel).
So, if S=0, L has to be even (symmetric space wave-function) and if S=1 L has to be odd (antisymmetric space wave-function) in order to respect Pauli exclusion. Sinthetically, this means L+S=even.
Since J=L+S=1, the possible combinations(*) are (L=0,S=1), (L=1,S=0 or 1), or (L=2,S=1). Of these combination, the only one with L+S=even is (L=1,S=1).
Parity of the final state is (-1)^L=-1. Parity of fermions is arbitrary (only parity of fermion+antifermion is defined, and it's -1) but in any case we have two, and P(n)*P(n)=+1.
So, P(π)=-1.

(*) for the sum of angular momenta in quantum mechanics, see for example here:
Suppose we combine two systems together, one with angular momentum j, the other with angular momentum j'. The resulting composite system will have angular momentum equal to one of the values:

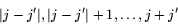
Since in our case we know that L+S=1 and S can be 0 or 1, we deduce that L=0, 1, or 2.

Parity of the neutral pion:
It's extracted from the polarization of the photons in π⁰ -> γγ.
The initial state has S=0, and the final state consists of identical bosons (exchange symmetry).
We want to write the wavefunction of the final state as a function of three orthogonal vectors: the polarization vectors of the two photons, and the direction of the photons in the pion rest frame. In fact, light has transverse polarization and so the polarization vectors are orthogonal to this direction.
The simplest possibilities, respecting the exchange symmetry, are:

1. proportional to the scalar product of the polarizations: this is proportional to the cosine of the angle (φ) between the planes of polarization; it's invariant under spatial inversion (scalar);
2. proportional to the triple product (vectorial product times scalar product) of all the three orthogonal vectors considered; this goes as the sine of φ, and changes sign under spatial inversion (pseudoscalar).

Charge conjugation:
Charged pions are not eigenstates of C, since Cπ⁺ -> π^-.
Instead, the π⁰ is an eigenstate of C. What is its eigenvalue?
This is found by the consideration that π⁰ -> γγ. And since C(γ)=-1 (electromagnetic fields are produced by moving charges that change sign under C), C(π⁰)=+1.
From this follows that π⁰ -> 3γ is forbidden (and in fact is not observed).