
or more conveniently:

Maximizing the likelihood is equivalent to minimizing -log(L), so one obtains the usual formulas for the best estimators of μ (the arithmetic mean) and of σ (the RMS).
If measurements y have been performed, and p(y|x) is the normalized probability density of y as function of parameters x, then the parameters x can be estimated by maximizing the joint probability density for the m measurements yj (assumed to be independent):
L(y|x)=Πj=1,...,mp(yj|x)
L is a measure for the probability of observing the particular sample y at hand, given x. Maximizing L by varying x amounts to interpreting L as function of x, given the measurements y.
Example 1: gaussian distribution

or more conveniently:

Maximizing the likelihood is equivalent to minimizing -log(L), so one obtains the usual formulas for the best estimators of μ (the arithmetic mean) and of σ (the RMS).
Example 2: tossing a coin (binomial statistics)
Consider tossing an unfair coin 80 times. Call the probability of tossing a HEAD p, and the probability of tossing TAILS 1-p. The parameter that we want to estimate is p.
The likelihood of the hypotheses p=1/3, p=1/2 and p=2/3 is:

The likelihood as a function of p:

We look for the maximum of this function by differentiating in p:
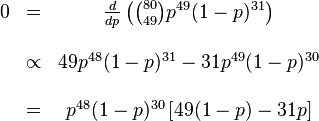
This equation has three solutions: 0, 1 and 49/80. The maximum value of L corresponds to p=49/80 (L=0 for p=0 and p=1).
Likelihoods for classification:

Multivariate analysis in the search for top quark (1994)
The likelihood function is approximated as:
f(x)=(normalization)*Σi=1N.eventsΠj=1N.observables K(xij,hj)
where K is a kernel which they take to be a multivariate gaussian centered at each data point xij with variance hj.
The Bayes discriminant is R(x)=fsignal(x)/fbkg(x)