BaBar primer on CP violation
CP violation and future B-factories

Main difference with the K system:
in K, the mass difference is very small but the lifetimes are very different, so it makes sense to characterize them as "short" and "long";
in B, the masses are different and they are characterized as "heavy" and "light".

Two-time formalism:
At PEP, coming from the Y(4s) resonance, the two B's are produced with L=1, so they are entangled (in the EPR sense). This means that at any moment there is a B0 and an anti-B0, whatever is their evolution.
But after one of the two B's is decayed, the other will continue to evolve.
So, the first decay can be taken as the start of the chronometer, at which the flavour (B or anti-B) is probed.
The oscillation probability goes like sin[Δm_B(t1-t2)/2].
The decay probability instead has a term exp[-Γ(t1+t2)].
It's not important which is the greatest between t1 and t2 (changing the sign is just a 180 degrees phase).
The CP amplitudes are integrated over t, from (t_CP-t_tag) to infinity(*).
The reason why PEP is asymmetric is to have the largest possible resolution on (t1-t2) from the vertex distance measurement.

(*) At hadron colliders the B's are produced incoherently and so the integral goes from 0 to infinity.

To study CP asymmetries one looks for events where one B decays to a CP eigenstate (f_CP) and the other into a state which tags the flavour with little ambiguity (f_tag).

Three types of CP violation in B decays:

1. In decay (or Direct CP violation): it happens both for charged and neutral B's.
2. In mixing: only in neutral B's. It occurs because the mass eigenstates are not flavour eigenstates.
3. In decay/mixing interference: it occurs in decays into final states that are common to both B0 and anti-B0.

1. In decay:
The modulus of the ratio of the amplitudes for B->f and anti-B->anti-f is a good variable to characterize the degree of CP violation, since its independent from conventions about the phase.
We assume that several amplitudes contribute to B->f.
Each amplitude has three parts: magnitude (A_i), weak phase term (e^iφ_i), strong phase term (e^iδ_i).
Between the two total amplitudes there is the CP phase:
A(B->f)=Σ_i A_ie^{i(+φ_i+δ_i)}
A(anti-B->anti-f)=e^{2i(ξ_f-ξ_B)}Σ_i A_ie^{i(-φ_i+δ_i)}
where, if f is a CP eigenstate, e^{2i(ξ_f-ξ_B)} = +1 or -1.
It has to be noted that the strong phase term is the same in both cases, while φ_i changes sign.
It can be seen (page 13 of the primer, eq. 1.46) that in order to detect CP violation, at least two terms with different weak phase have also different strong phase. So, in taking the ratio with the CP conjugated process, this will not cancel away.
(In this sense direct CP violation is an interference effect.)
Calculation of the strong phases is difficult and leads to large theoretical errors.

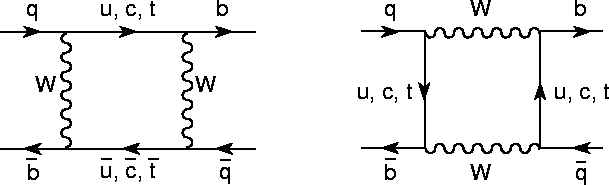
2. In mixing:
When CP is conserved, the mass eigenstates are also eigenstates of CP. (This is because H and CP commute.)
In this case, the relative phase between M₁₂ and Γ₁₂ is zero.
So, the quantity to be measured is the modulus of the ratio between M₁₂-iΓ₁₂ and its complex conjugate.
One way is to observe the asymmetry between B->l⁺ and anti-B->l^-
Theoretical uncertainties are big and so it's difficult to relate this observation to fundamental parameters.

3. In interference:
Take a final state f_CP, which is CP eigenstate and is accessible from both B and anti-B.
Just see if there is an asymmetry between B->f_CP and anti-B->f_CP.
Here there are no strong phases to calculate.

If you find a decay channel into a CP eigenstate in which only one diagram contributes, you can construct a CP asymmetry variable which is related to a single angle of the unitarity triangle.

Example 1: B_d⁰->J/ψK_s⁰

Number of B_d⁰ decaying at time t:

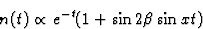
Number of anti-B_d⁰ decaying at time t:

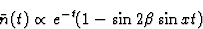
where x=ΔM/Γ~0.67.
CP asymmetry, time dependent:

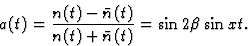
At PEP, where the B pair is produced in a definite CP state, integrating these asymmetries over time gives 0 (in fact one has to actually measure t).

Example 2: B_d⁰->π⁺π^-

This is related to sin 2α (lenght of the segment connecting (1,0) to (ρ,η)), but there are extra theoretical difficulties due to the extra gluon in the penguin.

Advantages of hadronic machines: bb cross section is orders of magnitude higher, possibility to study B_s mesons. Advantage of LHC over Tevatron and HERA: increasing the CM energy, the bb/total-inelastic ratio increases.

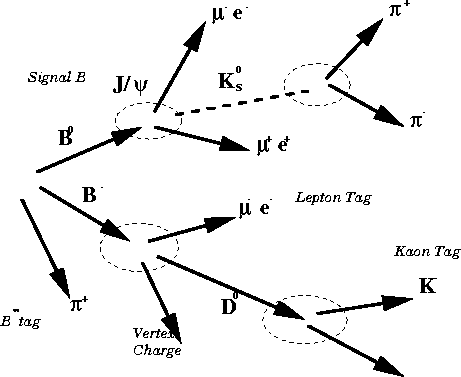
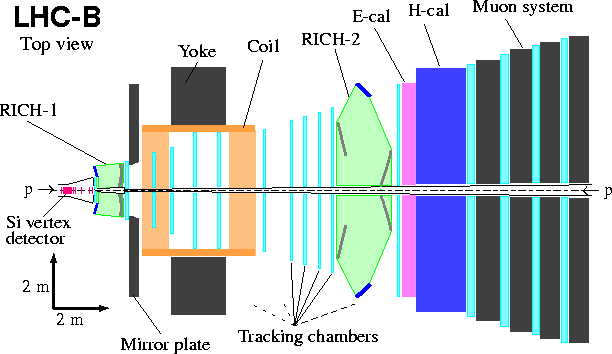
Experiments:

HERA-B: it's a fixed target experiment at HERA. The target is a wire, in the beam halo.
It is a single dipole spectrometer. It uses a vertex locator (different technologies for different distance from the wire), a RICH for K-tagging and a TRD to improve electron-tagging; an electromagnetic calorimeter is used (sampling; lead/scintillator and tungsten/scintillator). At the end there are conventional muon chambers.

LHC-B will defocus the beam in order to not have too many interactions per bunch crossing. It only observes one of the B mesons.